Wurm Universe
This is the first part of a series of articles on the "physics and astronomy" of the universe of Wurm Online, trying to describe the structure, dynamics and “laws of nature” of our in-game world . The information compiled here has been carefully researched and discussed by a small group of players who call themselves “The Wurm Astronomical Society” (Docterchese, McGarnicle, Valdor, WojorowskiPL and Yaga).
Part 1: Basic Metrics
(Basic dimensions of the Wurm universe: tiles, distances, slopes and heights)
The most basic unit of measurement is defined by the size of a “tile”. Tiles are the equally sized squares that the landscape of Wurm Online is entirely composed of. In the 3D world of Wurm a tile can be either flat or inclined, so that one or more of its corners can be higher or lower than the others.
In all our calculations we used the following fundamental information, given in the Wurmpedia (http://www.wurmpedia.com/index.php/Tile):
“A tile is a 4 meter by 4 meter square”.
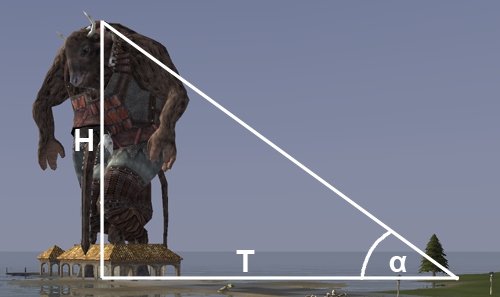
How can we measure distances and heights in Wurm? Originally we tried to use a spyglass, because it displays the distance between the observer and an object pointed to by the crosshairs:
Using a spyglass is sufficient to verify the basic unit of measurement (1 tile = 4m x 4m) and to measure linear distances within a reasonable accuracy. However, when it comes to measuring heights it turned out that a spyglass is not quite accurate enough to yield reliable results. Thus we need to use a more precise method: triangulation! This method uses basic trigonometric functions to determine the height of an object.
To determine the height H of an object, you define a reference point, take a screenshot (as shown in the example) and measure the angle α between the ground and the top of the object, as seen from the reference point. (As we have no means to measure angles in-game, we need to use a graphics program to determine the angle on the screenshot.) Additionally you need to measure the horizontal distance, which you obtain by counting the number of tiles T (remember: one tile corresponds to a distance of 4 meters). You then get the height H by using this formula:
H = T tan α
Here is an example: For a distance of 40 tiles (T=160m) we measure an angle of 14°. Thus, our avatar of Magranon would have a height of:
H = 160m ● tan(14°) = 40m
(Please note that the result has to be rounded, due to the immanent inaccuracy of this method.) Here is a list of heights for some arbitrary objects, just to give some examples:
| Object | Height (m) |
|---|---|
| Player character | 1.7 |
| House wall | 3.0 |
| Pillar | 5.6 |
| Freedom tower (incl. flag) | 25 |
| Colossus | 34 |
| Deity avatar | 40 |
Finally, talking about measuring heights, we must look at another basic unit of measurement used in the Wurm universe: “dirts”. Whenever we see sloped tiles defining the 3D landscape the elevation of slopes is given in terms of the amount of “dirts dropped”. When terraforming the land you use a shovel to dig or drop dirt - you add or subtract one “unit of dirt” with each action of the shovel.
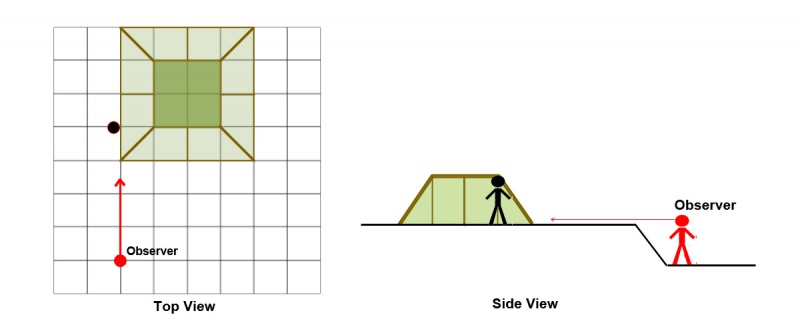
Using the method of triangulation described above we can find out how these “units of dirt” correspond to metric units. By dropping dirt we make elevated platforms of various heights, thus creating different slopes. We then position an observer in a pit, so that the eye level is slightly above the ground, and take screenshots:
Measuring the angles and using the formula given above, we can triangulate the elevation of the platform:
We obtain the following table (for slopes spanning a single tile):
| Slope | Angle | Elevation (m) |
|---|---|---|
| 10 | 14.0 | 1.0 |
| 20 | 26.6 | 2.0 |
| 30 | 36.9 | 3.0 |
| 40 | 45.0 | 4.0 |
| 50 | 51.3 | 5.0 |
| 60 | 56.3 | 6.0 |
| 70 | 60.3 | 7.0 |
| 80 | 63.4 | 8.0 |
| 90 | 66.0 | 9.0 |
| 100 | 68.2 | 10.0 |
| 150 | 75.1 | 15.0 |
| 200 | 78.7 | 20.0 |
Thus, there is a simple relation between “dirts” and metric units:
1 meter = 10 dirts.
Using this method it is also possible to determine the height of a player character with sufficient accuracy: